Question

A data set consists of the values 2, 6, 3, and 1. If we consider this a population (all the values available), the variance isA. 12

B. 14
C. the square root of 3.5
D. the square root of 14
E. none of the above

Answer 1

Answer: E. none of the above

Explanation:

The given data values that represents the population:

2, 6, 3, and 1.

Number of values : n=4

Mean of the data values =
`\frac{\text{Sum of values}}{\text{No. of values}}`

`(2+6+3+1)/(4)=(12)/(4)=3`

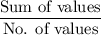
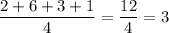
Sum of the squares of the difference between each values and the mean =

`(2-3)^2+(6-3)^2+(3-3)^2+(1-3)^2`

`=-1^2+3^2+0^2+(-2)^2`

`=1+9+0+4=14`

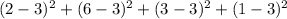
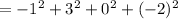
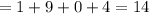
Now , Variance = (Sum of the squares of the difference between each values and the mean ) ÷ (n)

= (14) ÷ (4)= 3.5

Hence, the variance is 3.5.

Therefore , the correct answer is "E. none of the above".