The x-intercepts appear on this polynomial are 3 x intercepts.
Explanation:
To find the x intercepts of the polynomial
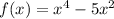 is by equating
is by equating
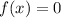
Thus, the equation becomes
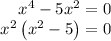
Equating, we get,
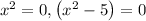
 ,
,
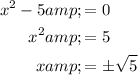
Thus, the x-intercepts are

Hence, the x-intercepts appear on this polynomial are 3 x intercepts.