Step-by-step explanation:
The given reaction is as follows.
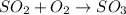
Now, balancing the given equation by putting appropriate coefficients.
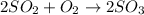
It is given that equimolar
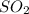 and
and
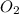 . Hence,
. Hence,
Therefore, during completion of the reaction,
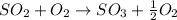
Temperature (T) =
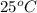 = (25 + 273) K = 298 K
= (25 + 273) K = 298 K
Pressure (P) = 1.75 atm
R (gas constant) = 0.0820 L atm/mol K
As on completion of reaction there is
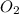 and
and
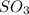 remains in the mixture. Therefore, molar mass of the mixture is equal to the sum of molar mass of
remains in the mixture. Therefore, molar mass of the mixture is equal to the sum of molar mass of
Total molar mass =
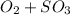
= (32 + 80) g/mol
= 112 g/mol
Hence, according to the formula we will calculate the density as follows.
Density =
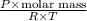
=
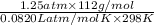
= 5.73 g/L
Thus, we can conclude that density of the product gas mixture is 5.73 g/L.