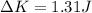Answers:
a)
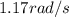
b)
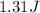
Step-by-step explanation:
a) We can solve this knowing the angular momentum
 is conserved, then:
is conserved, then:
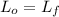
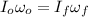 (1)
(1)
Where:
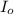 is the initial moment of inertia of the system
is the initial moment of inertia of the system
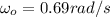 is the initial angular velocity
is the initial angular velocity
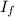 is the final moment of inertia of the system
is the final moment of inertia of the system
 is the final angular velocity
is the final angular velocity
But first, we have to find
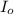 and
and
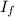 :
:
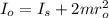 (2)
(2)
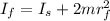 (3)
(3)
Where:
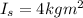 is the student's moment of inertia
is the student's moment of inertia
 is the mass of each object
is the mass of each object
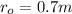 is the initial radius
is the initial radius
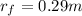 is the final radius
is the final radius
Then:
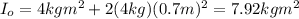 (4)
(4)
 (5)
(5)
Substituting the results of (4) and (5) in (1):
 (6)
(6)
Finding
 :
:
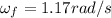 (7) This is the final angular velocity
(7) This is the final angular velocity
b) The rotational kinetic energy is:
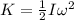 (8)
(8)
The change in kinetic energy is:
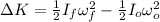 (9)
(9)
Since we already calculated these values, we can solve (9):
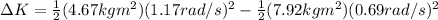 (10)
(10)
Finally: