Question

Find an equation for those points P such that the distance from P to A(0, 1, 2) is equal to the distance from P to B(6, 4, 2). What is this set?

Answer 1

Answer: The required equation for points P is
`4x+2y=17.`

Step-by-step explanation: We are give two points A(0, 1, 2) and B(6, 4, 2).

To find the equation for points P such that the distance of P from both A and B are equal.

We know that the distance between two points R(a, b, c) and S(d, e, f) is given by

`RS=√((d-a)^2+(e-b)^2+(f-c)^2).`

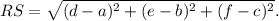
Let the point P be represented by (x, y, z).

According to the given information, we have

`PA=PB\\\\\Rightarrow √((x-0)^2+(y-1)^2+(z-2)^2)=√((x-6)^2+(y-4)^2+(z-2)^2)\\\\\Rightarrow x^2+y^2-2y+1+z^2-4z+4=x^2-12x+36+y^2-8y+16+z^2-4z+4~~~~~~~[\textup{Squaring both sides}]\\\\\Rightarrow -2y+1=-12x-8y+52\\\\\Rightarrow 12x+6y=51\\\\\Rightarrow 4x+2y=17.`

Thus, the required equation for points P is
`4x+2y=17.`