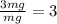Answer:
n/(FG) = 3.
Step-by-step explanation:
At the top of the loop-the-loop, the normal force is directed downwards as well as the weight of the car. So, the total net force of the car is
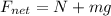
By Newton's Second Law, this force is equal to the centripetal force, because the car is making circular motion in the loop.
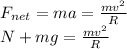
The critical speed is the minimum speed at which the car does not fall. So, at the critical speed the normal force is zero.
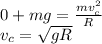
If the car is moving twice the critical speed, then
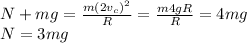
Finally, the ratio of the normal force to the gravitational force is