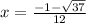The value of x is
 and
and
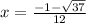
Explanation:
The equation is
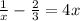
Subtracting by
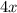 on both sides,
on both sides,
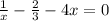
Taking LCM,
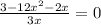
Multiplying by 3x on both sides,

Dividing by (-) on both sides,

Using quadratic formula, we can solve for x.
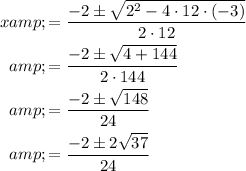
Taking out common term 2, we get,
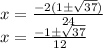
Thus, the value of x is
 and
and