Question

An SRS of 350 350 high school seniors gained an average of ¯ x = 22.61 x¯=22.61 points in their second attempt at the SAT Mathematics exam. Assume that the change in score has a Normal distribution with standard deviation σ = 53.63 . σ=53.63. We want to estimate the mean change in score μ μ in the population of all high school seniors. (a) Using the 68 68 – 95 95 – 99.7 99.7 Rule or the z - z- table (Table A), give a 95 % 95% confidence interval ( a , b ) (a,b) for μ μ based on this sample.

Answer 1

Answer: (16.9914, 28.2286).

Explanation:

The formula to find the confidence interval for population mean is given by :-

`\overline{x}\pm z^*(\sigma)/(√(n))`

, where
`\overline{x}` = Sample mean

`\sigma`= Population standard deviation

n= Sample size.

z* = Critical value.

Let μ be the mean change in score in the population of all high school seniors.

As per given , we have

n= 350

`\overline{x}=22.61`

`\sigma=53.63`

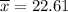
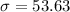
The critical z-value for 95% confidence interval is z*= 1.96 [From z-table]

Substitute all the value in formula , we get

`22.61\pm (1.96)(53.63)/(√(350))`

`=22.61\pm (1.96)(53.63)/(18.708287)`

`=22.61\pm (1.96)(2.8666)`

`=22.61\pm (5.6186)`

`=(22.61-5.6186,\ 22.61+5.6186) =(16.9914,\ 28.2286)`

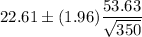
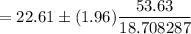
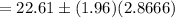
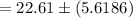
Hence, the 95% confidence interval for
`\mu` is (16.9914, 28.2286).