Answer:
The powers of a,b and c for the given expression
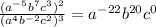 is -22,20 and 0 respectively
is -22,20 and 0 respectively
Explanation:
Given expression is
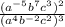
To find the powers of a,b and c:
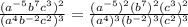 ( using the property
( using the property
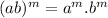 )
)
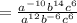 ( using the property
( using the property
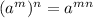 )
)
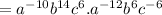 ( using the property
( using the property
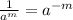 )
)
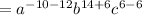 ( using the property
( using the property
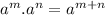 )
)
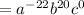
Therefore
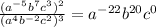
The powers of a,b and c for the given expression
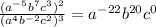 is -22,20 and 0 respectively
is -22,20 and 0 respectively