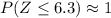Answer:
a)
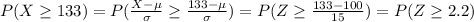
And we can find this probability using the complement rule:
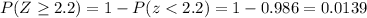
b)
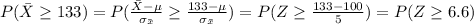
And we can find this probability using the complement rule:
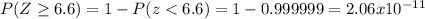
c) No. The mean can be lower than 131.5 if we find the probability:

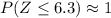
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
A. If 1 person is randomly selected from thegeneral population, find the probability of getting someone with anIQ score of at least 133.
Let X the random variable that represent the scores of a population, and for this case we know the distribution for X is given by:

Where
 and
and
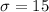
We are interested on this probability
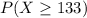
And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
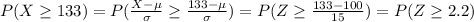
And we can find this probability using the complement rule:
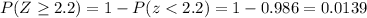
And the probability is calculated from the normal standard table or with excel.
B. If 9 people are randomly selected,find the probability that their mean IQ score is at least 133.
For this case since the distribution for the random variable X is normal then the distribution for the sample mean is also normal and given by:
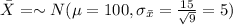
The new z score is defined as
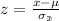
If we apply this formula to our probability we got this:
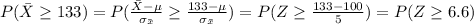
And we can find this probability using the complement rule:
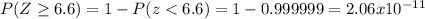
And the probability is calculated from the normal standard table or with excel.
C. Although the results are available,the individual IQ test scores have been lost. Can it be concluded that all 9 candidates have IQ scores above 131.5 so that they allare eligible for Mensa membership?
No. The mean can be lower than 131.5 if we find the probability: