Answer:
x1 =1
x2 =2
x3 =4
Explanation:
Given is a systems of equations in 3 variables.
No of equations given = 3
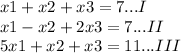
subtract equation 1 form equation 3
We get

Substitute this value in 2 and 3
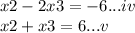
subtract iv from v
3x3 = 12
x3=4
Substitute in v
x2 =2
solution is
x1 =1
x2 =2
x3 =4