Answer:
Part A)
About $3767.34.
Part B)
About $3692.47.
Explanation:
Part A)
Recall that compound interest is given by the formula:

Where A is the final amount, P is the initial amount, r is the interest rate, n is the number of times compounded per year, and t is the number of years.
To obtain $4000 after two years, let A = 4000 and t = 2.
Because the account pays 3% interest compounded monthly, r = 0.03 and n = 12.
Substitute and solve for P:
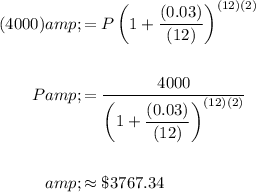
In concluion, about $3767.34 should be deposited.
Part B)
Recall the formula for continuous compound:
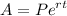
Where e is Euler's number.
Hence, let A = 4000, r = 0.04 and t = 2. Substitute and solve for P:

In conclusion, about $3692.47 should be deposited.