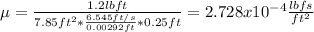Question

The viscosity of a fluid is to be measured by an viscometer constructed of two 5 ft long concentric cylinders. The inner diameter of the outer cylinder is 6 in, and the gap between the two cylinders is 0.035 in. The outer cylinder is rotated at 250 rpm, and the torque is measured to be 1.2lbf *ft.

A) Determine the viscosity of the fluid.

Answer 1

`\mu= (1.2 lb ft)/(7.85ft^2 * (6.545 ft/s)/(0.00292ft) *0.25 ft)=2.728x10^(-4) (lbf s)/(ft^2)`

Step-by-step explanation:

For this case we need to remember first thet the torque T is defined as:

`T = FR`

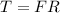
Where T represent the torque, F the force acting in the inner cylinder and R the radius for the inner cylinder.

For the inner cylinder the force acting can be expressed as:

`F = \mu A (v)/(l)`

Where
`\mu` represent the viscosity of the fluid, A the area of the inner cylinder, v represent the tangential velocity and l the thickness of fluid between the two cylinders.

And the tangential velocity for this case can be esxpressed as
`v = wR`

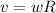
The info given is:

`l = 0.035 in *(1ft)/(12in)=0.00292 ft`

`R= (D)/(2) =(6 in)/(2)= 3 in*(1ft)/(12 in)=0.25 ft`

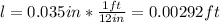
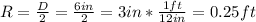
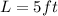`L = 5 ft` from the info given

N= 250 rpm represent the reveolutions per minute

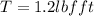`T = 1.2 lbf ft` represent the torque given

We can find the surface area for the cylinder with this formula:

`A= 2\pi R L`

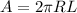
And if we replace we got:

`A= 2\pi 0.25 ft *5 ft= 7.85 ft^2`

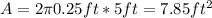
Now we can find the tangential velocity like this:

`v=wR= \frac2\pi *250 rpm* (1min)/(60s) * 0.25 ft=6.55(ft)/(s)`

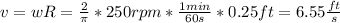
Now we can set up the following equation for the torque:

`T = FR`

`T = \mu A (v)/(l) R`

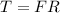
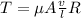
And we can find the value for the viscosity
`\mu` like this:

`\mu = (T)/(A (v)/(l) R)`

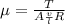
And if we replace we got:

`\mu= (1.2 lb ft)/(7.85ft^2 * (6.545 ft/s)/(0.00292ft) *0.25 ft)=2.728x10^(-4) (lbf s)/(ft^2)`