Question

Find the unit tangent vector T(t) at the point with the given value of the parameter t. r(t)

Answer 1

To find the unit tangent vector, we first need to find the velocity vector. Given that the position vector is r(t) = Acos(wt)i + Asin(wt)j, we can find the derivative of this vector to get the velocity vector. To find the unit tangent vector, we divide the velocity vector by its magnitude.

Step-by-step explanation:

To find the unit tangent vector, we first need to find the velocity vector. Given that the position vector is r(t) = Acos(wt)i + Asin(wt)j, we can find the derivative of this vector to get the velocity vector:

v(t) = -Aw*sin(wt)i + Aw*cos(wt)j

To find the unit tangent vector, we divide the velocity vector by its magnitude:

T(t) = (v(t))/(|v(t)|) = (-Aw*sin(wt)i + Aw*cos(wt)j)/(sqrt((Aw*sin(wt))^2 + (Aw*cos(wt))^2))

So, the unit tangent vector at any point is T(t).

Answer 2

Since the equation was missing, I solved it with another equation and got an answer of T(0) = <3j / 5 + 4k / 5>.

Please see my explanation. I hope this helps

Step-by-step explanation:

The question asked us to find out unit tangent vector.

Recall unit vector = vector / magnitude of vector

Since the question is missing with an equation. I suppose an equation.

r(t)=Cost i, 3t j, 2Sin(2t) k at t=0

Lets take out differentiation

r'(t) = <(-Sint), 3, 2(Cos(2t)(2))>

r'(t)= <-Sint, 3, 4Cos(2t)>

Now substitute t=0 in the differentiate found above.

r'(0)= <-Sin(0), 3, 4Cos(2*0)>

r'(0)= <0, 3, 4(1)>

r'(0)= <0,3,4>

vector r'(0)=<0i, 3j, 4k>

Now lets find out magnitude of vector

|r'(0)| =
`\sqrt{0^(2)+3^(2)+4^(2) }`

|r'(0)| =
`√(0+9+16)`

|r'(0)| =
`√(25)`

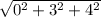
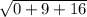
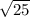
|r'(0)| = 5

Unit Tangent Vector

T(0) = <0, 3, 4> / 5

T(0) = <3j / 5 + 4K / 5>