Answer:
$600
Explanation:
Let the random variable
 denote the damage in $ incurred in a certain type of accident during a given year. The probability distribution of
denote the damage in $ incurred in a certain type of accident during a given year. The probability distribution of
 is given by
is given by
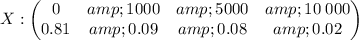
A company offers a $500 deductible policy and it wishes its expected profit to be $100. The premium function is given by
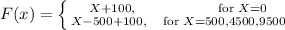
For
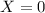 , we have
, we have
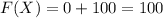
For
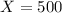 ,
,
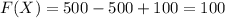
For
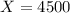 ,
,

For
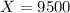 ,
,
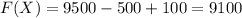
Therefore, the probability distribution of
 is given by
is given by
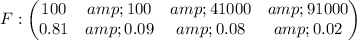
To determine the premium amount that the company should charge, we need to calculate the expected value of
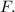
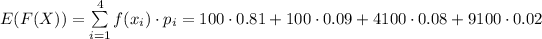
Therefore,
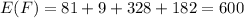
which means the $600 is the amount the should be charged.