Question

two cards are chosen at random from a deck of 52 playing cards. what is the probability that they are both aces?

Answer 1

The probability that they are both aces is 0.00452.

Explanation:

Consider the provided information.

Out of 52 playing card we need to select only 2.

Thus, the sample space is:
`^(52)C_2=1326`

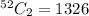
Two cards are Ace.

The number of Ace in a pack of playing card are 4 and we need to select two of them.

This can be written as:
`^4C_2=6`

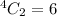
Thus, the probability that they are both aces is:

`P(\text{Both are Ace})=(6)/(1326) \approx0.00452`

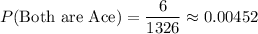
Hence, the probability that they are both aces is 0.00452.