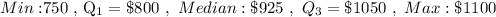Question

The Insurance Institute for Highway Safety publishes data on the total damage caused by compact automobiles in a series of controlled, low-speed collisions. The following costs are for a sample of six cars:

$800, $750, $900, $950, $1100, $1050.
1. What is the five-number summary of the total damage suffered for this sample of cars?

Answer 1

Answer:
`Min : $750\ ,\ Q_1= \$800\ ,\ Median : \$925\ ,\ Q_3=\$1050\ ,\ Max: \$1100`

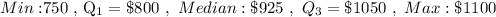
Explanation:

The five -number summary consists of five values :

Minimum value , First quartile
`(Q_1)` , Median , Third Quartile
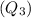`(Q_3)` , Maximum value.

Given : The Insurance Institute for Highway Safety publishes data on the total damage caused by compact automobiles in a series of controlled, low-speed collisions.

The following costs are for a sample of six cars:

$800, $750, $900, $950, $1100, $1050.

Arrange data in increasing order :

$750,$800, $900, $950, $1050, $1100

Minimum value = $750

Maximum value = $1100

Median = middle most term

Since , total observation is 6 (even) , so Median = Mean of two middle most values ($900 and $950).

i.e. Median
`=(900+950)/(2)=\$925`

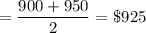
First quartile
`(Q_1)` = Median of lower half ($750,$800, $900)

= $800

, Third Quartile
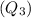`(Q_3)` = Median of upper half ($950, $1050, $1100)

= $1050

Hence, the five-number summary of the total damage suffered for this sample of cars will be :

`Min : $750\ ,\ Q_1= \$800\ ,\ Median : \$925\ ,\ Q_3=\$1050\ ,\ Max: \$1100`