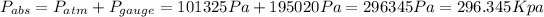Question

Derive a relationship between depth and temperature, then substitute that into the density/temperature relationship and use the equation from the text to solve the integral and pressure difference. What is the gage pressure at the bottom of the lake?What is the absolute pressure at the bottom of the lake?

Answer 1

`P_(gauge)= 195020 Pa= 195.02 Kpa`

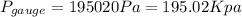
And the absolute pressure at the bottom would be:

`P_(abs)= P_(atm) +P_(gauge)= 101325 Pa +195020 Pa= 296345 Pa= 296.345 Kpa`

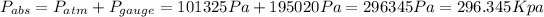
Explanation:

From the figure attached we know the following two conditions:

`Z=0 , T=40C`

`Z=20 , T=4`

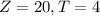
And we want a linear model like this one:

`T = mZ +b`

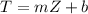
Where m abd b represent the slope and intercept.

We can find the slope with the following expression:

`m =(4-40)/(20-0)= -(9)/(5)`

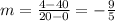
And then we can find the intercept using the first point:

`40 = -(9)/(5) *0 +b  , b= 40`

So then the linear model is:

`T = -(9)/(5) Z +40`

Assuming the following formula for the density:

`\rho_(H2O) = 1 +(T-40)/(3600)`

If we replace the expression for T into the density we got:

`\rho_(H2O) = 1+ (-(9)/(5) Z +40 -40)/(3600)`

`\rho_(H2O) = 1 -(z)/(2000)`

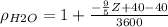
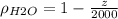
Since the units for
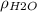`\rho_(H2O)` are g/ml we can convert this into kg/m^3 multiplying by 1000 and we got:

`\rho_(H2O) =1000- (z)/(2)`

Then we have the following differential equation:

`(dP)/(dz) = -\rho g`

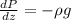
If we replace the expression for the density in terms of z we got:

`(dP)/(dz) = ((z)/(2) -1000) g`

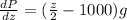
And we can separate like this:

`dP = ((z)/(2) -1000) g dz`

Now w can integrate both sides and we got:

`\Delta P = g[((\Delta z)^2)/(4) -1000\Delta z]`

And that would be the expression for the change of pressure:

For our case we have 20m of difference between the surface and the bottom so then the change of pressure between these two levels is:

`\Delta P= 9.8 (m)/(s^2) [((20m)^2)/(4) -1000(20m)]= -195020 Pa`

We know that the pressure increase with the depth. So then the gage pressure at the bottom would be:

`P_(gauge)= 195020 Pa= 195.02 Kpa`

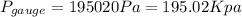
And the absolute pressure at the bottom would be:

`P_(abs)= P_(atm) +P_(gauge)= 101325 Pa +195020 Pa= 296345 Pa= 296.345 Kpa`