Question

The CHS baseball team was on the field in the batter popped the ball up the equation PT equals 80 T -16 T squared +3.5 represents the height of the bar above the ground in feet as a function of time in seconds how long will the catcher have to get in position to catch the ball before it hits the ground

Answer 1

The time the catcher have to get in position to catch the ball before it hits the ground is nearly 5 seconds.

Explanation:

Given:

The variation of height of a ball above ground with time 't' is given as:

`P(T)=80T-16T^2+3.5`

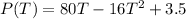
In order to reach the ground, the height will be 0 feet.

So, plugging in 0 for 'P(T)' and solving for time 'T', we get:

`P(T)=0\\80T-16T^2+3.5=0\\16T^2-80T-3.5=0`

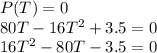
Solving for 'T' using the quadratic formula:

For a quadratic equation
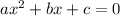`ax^2+bx+c=0`, the solutions are:

`x=(-b\pm√(b^2-4ac))/(2a)`

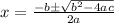
For the above equation,
`a=16,b=-80,c=-3.5`

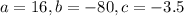
Therefore, the values of 'T' are:

`T=(-(80)\pm√((-80)^2-4(16)(-3.5)))/(2(16))\\\\\textrm{On solving, we get:}\\\\T=5.04\ s\ or\ T=-0.04\ s`

Negative time is neglected as time can't be negative.

Therefore, the time the catcher have to get in position to catch the ball before it hits the ground is nearly 5 seconds.