Question

Can someone help me with the problem in the image

Answer 1

PT=57

Explanation:

If PT=7x+8 and TQ=9x-6 qnd we have that T is the midpoint of PQ.

Since T is the midpoint of PQ,
`PT=TQ`

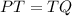
We substitute into the equation to get:

`7x+8=9x-6`

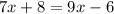
Group the similar terms to get:

`8+6=9x-7x`

We simplify now to get:

`14=2x`

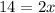
Divide through by 2 to get:

`x=7`

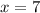
PT=7*7+8=49+8=57