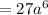Answer:
Explanation:
The question is not clear. So, assuming that the expression you need to simplify is this one:
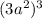
You need to remember a property called "Power of a power property". This property states the following:

Therefore, you need to apply the Power of a power property explained before, in order to simplify the expression provided in the exercise, multiplying the exponents inside the parentheses by the exponent outside of the parentheses. Then:
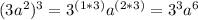
Now, you must remember that:
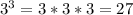
Finally, you get: