Answer:
Calvin's first step is to simplify the expression is to apply the quotient of powers to get (r Superscript negative 13 Baseline s Superscript negative 1 Baseline) Superscript negative 4 is the correct step
That is
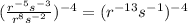 Calvin's step is the correct step.Because this is the correct way to do simplify the rational expression. And also because Nadine made a blender mistake in her operations in step
Calvin's step is the correct step.Because this is the correct way to do simplify the rational expression. And also because Nadine made a blender mistake in her operations in step
Explanation:
Given that Nadine and Calvin are simplifying the expression (StartFraction r Superscript negative 5 Baseline s Superscript negative 3 Baseline Over r Superscript 8 Baseline s Superscript negative 2 Baseline EndFraction) Superscript negative 4
Their expression can be written as below
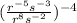
Nadine's first step is to simplify the expression is to raise the numerator and denominator to the power of 4 to get StartFraction r Superscript negative 20 Baseline s Superscript negative 12 Baseline Over r Superscript 32 Baseline s Superscript 8 Baseline EndFraction
That is

Calvin's first step is to simplify the expression is to apply the quotient of powers to get (r Superscript negative 13 Baseline s Superscript negative 1 Baseline) Superscript negative 4
That is
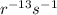
Now simplify the given expression to check whose step is correct:
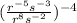
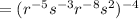 ( using the property
( using the property
 )
)
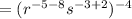

Therefore
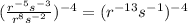
Therefore Calvin's first step is to simplify the expression is to apply the quotient of powers to get (r Superscript negative 13 Baseline s Superscript negative 1 Baseline) Superscript negative 4 is the correct step.
That is
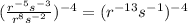 Calvin's step is the correct step .Because this is the correct way to do simplify the rational expression.And also because Nadine made a blender mistake in her operations in step
Calvin's step is the correct step .Because this is the correct way to do simplify the rational expression.And also because Nadine made a blender mistake in her operations in step