Question

A box, with rectangular sides, base and top is to have a volume of 2 cubic feet. It has a square base. Express the surface area A of the box in terms of the width w of the base. If the material for the base and top costs 30 dollars/ft^2 and that for the sides costs 40 dollars/ft^2 express the total cost C as a function of the width.

A(w)= _________ ft^2
C(w)= _________ $

Answer 1

`A(w)=2w^2+(8)/(w)`

`C(w)=60w^2+(320)/(w)`

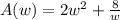
Explanation:

First of all you need to determine the height of the box. This can be done using the known volume of the box:

`V=2\ \text{ft}^2`

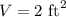
The equation for evaluating volume of a box is as follows:

`V=w^2h`

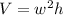
since it has a square base.

Now you solve this equation for height:

`h=(2)/(w^2)`

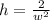
Now the surface area of the box is equals to:

`A=2w^2+4wh`

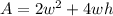
After you replace h with the above equation you get:

`A(w)=2w^2+(8)/(w)`

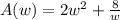
To find the total cost function with respect to width of the base you need to find the surface areas of the base and sides and multiplicate it with the relevant cost:

`C=30\cdot2w^2+40\cdot4wh`

After you replace h with the above equation you get:

`C(w)=60w^2+(320)/(w)`