Answer:
0.74 m/s
Step-by-step explanation:
given,
time taken by the ramp to cover cliff , t = 64 s
acceleration = 0.37 m/s²
distance traveled by the belt
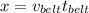
Clifford is moving with constant acceleration
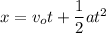 ...(1)
...(1)
initial velocity is equal to zero
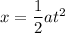 ........(2)
........(2)
equating equation (1) and (2)

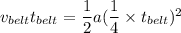
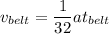
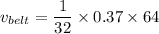
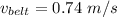
Speed of the belt is equal to 0.74 m/s