Question

What are the rectangular coordinates of the point whose cylindrical coordinates are (r=9, θ=2π3, z=3)(r=9, θ=2π3, z=3) ?

Answer 1

The point is
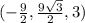`(-(9)/(2),(9√(3))/(2),3)` in rectangular coordinates.

Explanation:

To convert from cylindrical to rectangular coordinates we use the relations

`x=r \cdot cos(\theta)\\y=r\cdot sin(\theta)\\z=z`

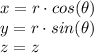
To convert the point
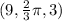`(9,(2)/(3)\pi ,3)` from cylindrical to rectangular coordinates we use the above relations

Since
`r=9`,
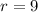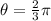`\theta=(2)/(3) \pi`, and
`z=3`,

`x=r \cdot cos(\theta)=9\cdot cos((2)/(3)\pi )=-(9)/(2)`

`y=r\cdot sin(\theta)=9\cdot sin((2)/(3) \pi )=(9√(3))/(2)`

`z=z=3`

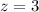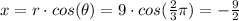
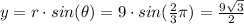
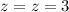
Thus, the point is
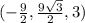`(-(9)/(2),(9√(3))/(2),3)` in rectangular coordinates.