Answer: C.
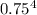
Explanation:
Let x be the binomial variable that denotes the number of makes.
Since each throw is independent from the other throw , so we can say it follows Binomial distribution .
So
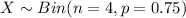
Binomial distribution formula: The probability of getting x success in n trials :
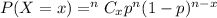 , where p = probability of getting success in each trial.
, where p = probability of getting success in each trial.
Then, the probability of Michael Beasley making all of his next 4 free throw attempts will be :
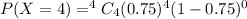
![=(1)(0.75)^4(1)\ \ [\because\ ^nC_n=1]\\\\=(0.75)^4](https://img.qammunity.org/2021/formulas/mathematics/college/djwrp37i8h4y4ud3ksgfgcafkds9uxroer.png)
Thus, the probability of Michael Beasley making all of his next 4 free throw attempts is
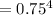
Hence, the correct answer is C.
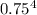 .
.