Question

A vehicle is moving in a straight line. The velocity Vms^-1 at time t seconds after the vehicle starts is given by V = A (t− 0.05t^2) for 0 ≤ t ≤ 15. What is the value of A?

Answer 1

Explanation:

Answer 2

The value of A is
`(-\infty, 0) \cup(0, \infty)`

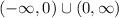
Explanation:

Given:

`V = A (t- 0.05t^2)`

When velocity V= 0

we have

`A (t- 0.05t^2) = 0`

`(t- 0.05t^2) = 0`

`t = 0.05t^2`

t =0 , t =
`(1)/(0.05)`

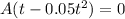
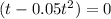
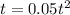
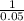
t = 0 , t = 20

So when we draw a graph,The resulting graph will be a quadratic graph.

`(dv)/(dt) = A[1 - 0.1t]`

`(dv)/(dt) = 0`

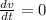
t=10 sec

At t=10, the velocity will be

`v(10) = [10 -0.05(10)^2]`

`v(10) = [10 -5]`

`v(10) = 5A`

But according to the question A is not dependent on t

So A can be any value other than zero