Question

The popcorn stand sells only soft drinks and popcorn, and only one size of each. In fact, the same cup is used for both products this is part of the stand's "sales pitch. "A soft drink cost $2.00 and a popcorn cost $4.00. On a certain day, 120 cups were used and $330.00 was collected. How many soft drinks and how many popcorns were sold on that day? Use a system of equations approach to find your answer. Show all work.

Answer 1

On that day 75 soft drinks and 45 popcorn were sold.

Explanation:

Given:

Let the number of soft drinks be 'x'.

Let the number of popcorn be 'y'.

Number of cups sold = 120

Now we know that;

Number of cups sold is equal to sum of the number of soft drinks and the the number of popcorn.

framing in equation form we get;

`x+y=120 \ \ \ \ equation \ 1`

Also Given:

Cost of Soft drink = $2 .00

Cost of popcorn = $4.00

Total amount collected = $330.00

Now we know that;

Total amount collected is equal to sum of the number of soft drinks multiplied by Cost of Soft drink and the number of popcorn multiplied Cost of popcorn.

framing in equation form we get;

`2x+4y = 330 \ \ \ \ eqaution \ 2`

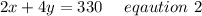
Hence The System of equation to determine the number of softdrinks and cups sold is
`\left \{ {{x+y=120} \atop {2x+4y=330}} \right.`.

Now to find the number of each type of cups sold we will solve the above equations.

First we will multiply equation 1 with 2 we get;

`2(x+y)=120*2\\\\2x+2y =240 \ \ \ \ equation \ 3`

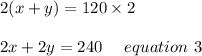
Now we will subtract equation 3 from equation 2 we get;

`2x+4y-(2x+2y)=330-240\\\\2x+4y-2x-2y=90\\\\2y = 90`

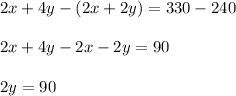
Now Dividing both side by 2 we get;

`(2y)/(2)= (90)/(2)\\\\y=45`

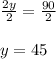
Now we will substitute the value of 'y' in equation 1 we get;

`x+y=120\\\\x+45 =120\\\\x=120-45 = 75`

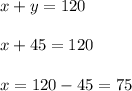
Hence On that day 75 soft drinks and 45 popcorn were sold.