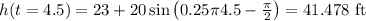Question

Write an equation about the movement of a Ferris wheel.As a Ferris wheel turns , the distance a rider is above the ground varies sinusoidally with time. The highest point on the wheel is 43 feed above the ground. The wheel makes a full circle every 8 seconds and has a diameter of 40 feet. Sketch a graph of your height as a rider as a function of time.a. What is an equation for your graph?b. Use this equation to predict your height above the ground at 4.5 seconds.

Answer 1

Explanation:

The graph is sketched in the attachment. It's easy to sketch the same graph using the given information. Let's say h is the height. For time t=0 you put a dot on 3 feet since it's the lowest point of the ferris wheel (you get that by substracting the diameter of 40 feet from the highest point given (43 feet).

Second dot is your highest point 43 feet at t=4 sec since it is the half of the circle.

The third dot is your lowest point again at t=8 sec. If you connect the dots like a sine you get the sketched graph.

To find out what is the equation for the graph you need to look at the amplitude which in this case is 20 feet. Then you need to find out the frequency at which the wheel is turning. Since you are given the period (8 sec for a full cycle) you get the frequency:

`f=(1)/(T)=(1)/(8)`

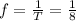
Now you need to find out the phase of the wave. Since we want to be at 0 feet at t=0 you need to shift the wave 90° degrees forward or
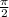`(\pi)/(2)` in radians.

Finally it's important to shift the whole wave up. You do that by adding the appropriate amount that is in this case the half of the diameter plus the 3 feet to the ground.

The equation you get is:

`h(t)=23+A\sin(2\pi f t-\phi)=23+20\sin(0.25\pi t-(\pi)/(2))`

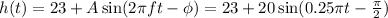
where A is amplitude,
`\phi` is the phase shift and
`f` is the frequency.

Finally you can get the height at
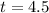`t=4.5` sec:

`h(t=4.5)=23+20\sin\left(0.25\pi4.5-(\pi)/(2)\right)=41.478\ \text{ft}`