Answer:
- Echelon form.
- Reduced Echelon form.
- Neither.
Explanation:
The objective is to determine which of the following matrices are in reduced echelon form and which others are only in echelon form. The given matrices are
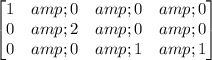 ,
,
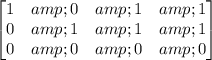 and
and
 .
.
First, recall what is an echelon and reduced echelon form of a matrix.
A matrix is said to be in a Echelon form if
- If there is any zero rows, all nonzero rows are placed above them;
- Each first non-zero entry in a row, which is the leading entry, is placed to the right of the leading entry of the row above it;
- All elements below the leading entry must be equal to zero in each column.
A matrix is said to be in a Reduced Echelon form if
- In each non-zero row, the leading entry is 1.
- In its column, each leading 1 is actually the only non-zero element.
A column that contains a leading 1 which is the only non-zero element is called a pivot column.
Now, let's have a look at the first matrix
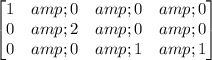
As we can see, it doesn't have any zero rows. Each leading entry in a row is placed to the right of the leading entry from the row above and all elements below the leading entries in all columns are equal to zero. Therefore, this matrix is in an Echelon form.
In the second row, the leading entry is 2, not 1, so because of the first property of the Reduced Echelon form, it is not in a Reduced Echelon form.
Notice that it can be transformed to the Reduced Echelon form by multiplying the second row by
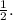
The second matrix is
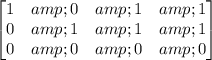
There is a zero row, and all non-zero rows are placed above it. Each leading entry in a row, which is the first non-zero entry, is placed to the right of the entry of the row above it and all elements below the leading entry are equal to zero in each column, so it is in the Echelon form.
It is also in the Reduced Echelon form, since all non-zero rows the leading entry is 1 and it is the only non zero element in each column.
The least given matrix is

This matrix doesn't satisfy the condition that if there is any zero-row, it must be below all other non-zero rows, so it is not in Echelon form.
A matrix that is not in an Echelon form, it is not in an Reduced Echelon form either.
Therefore, this matrix is not in an Reduced Echelon form.