Question

The Aye-Aye exhibits incomplete dominance for eye color. In a population of Aye-Ayes there are red-eyed individuals exhibiting the dominant phenotype and yellow-eyed individuals exhibiting the recessive phenotype. If there are 66 yellow-eyed individuals in the current population of 459, how many would be expected to exhibit the heterozygous phenotype in the next generation which will consist of 410 total individuals?

Answer 1

196.8

Step-by-step explanation:

In a population of Aye-Ayes there are red-eyed individuals exhibiting the dominant phenotype -----i.e RR

yellow-eyed individuals exhibiting the recessive phenotype ----- i.e rr

in the next generation, we will have the following offspring

R R

r Rr Rr

r Rr Rr

All the offspring are heterozygous in nature.

Now, the question goes further by saying, if there are 66 yellow-eyed individuals in the current population of 459, i.e (q² =66)

How many would be expected to exhibit the heterozygous phenotype in the next generation which will consist of 410 total individuals.

In solving Hardy-Weinberg question, we use the following equation below.

p + q = 1

p² + 2pq + q² = 1

where;

p = the frequency of the dominant allele

q = the frequency of the recessive allele

p² = the frequency of individuals with homozygous dominant phenotype

2pq = the frequency of individuals with heterozygous phenotype

q² = frequency of individuals with the homozygous recessive phenotype

Now, If In the next generation, the total population = 410

and q² (yellow-eyed individuals that are recessive in nature) = 66

then; q²=
`(individuals with recessive phenotype)/(total population)`

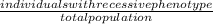
q² =
`(66)/(410)`

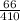
q² = 0.16

q =
`√(0.16)`

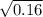
q = 0.4

Since q = 0.4, we can easily get p by using the formula above:

p + q = 1

p = 1 - q

p = 1 - 0.4

p = 0.6

∴ Since we've known our p and q , we can easily determine how many would be expected to exhibit the heterozygous phenotype in the next generation.

2pq = 2 ( 0.6 × 0.4)

= 2 ( 0.24)

= 0.48

2pq =
`(individuals with heterozygous phenotype)/(total population)`

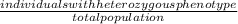
0.48 =
`(x)/(410)`

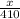
x = 0.48 × 410

x = 196.8 individuals