Question

Find the​

(a) mean,​
(b) median,​
(c) mode, and​
(d) midrange for the given sample data.
An experiment was conducted to determine whether a deficiency of carbon dioxide in the soil affects the phenotype of peas. Listed below are the phenotype codes where 1 equals smooth dash yellow1=smooth-yellow​, 2 equals smooth dash green2=smooth-green​, 3 equals wrinkled dash yellow3=wrinkled-yellow​, and 4 equals wrinkled dash green4=wrinkled-green. Do the results make​ sense?
11 44 44 44 22 11 44 33 11 44 44 33 33 11
​(a) The mean phenotype code is 2.82.8. ​(Round to the nearest tenth as​ needed.) ​
(b) The median phenotype code is 33. ​(Type an integer or a​ decimal.)
​(c) Select the correct choice below and fill in any answer boxes within your choice.
A. The mode phenotype code is 44. ​(Use a comma to separate answers as​ needed.)
B. There is no mode.
​(d) The midrange of the phenotype codes is 2.52.5. ​(Type an integer or a​ decimal.)
Do the measures of center make​ sense?
A. Only the​ mean, median, and mode make sense since the data is numerical.
B. Only the​ mean, median, and midrange make sense since the data is nominal.
C. Only the mode makes sense since the data is nominal.
D. All the measures of center make sense since the data is numerical.

Answer 1

a) Mean = 2.8

b) Median = 3

c) Mode = 4

d) Mid range = 2.5

e) Option C) Only the mode makes sense since the data is nominal.

Explanation:

We are given the following data set in the question:

1, 4, 4, 4, 2, 1, 4, 3, 1, 4, 4, 3, 3, 1

a) Mean

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(39)/(14) = 2.78 \approx 2.8`

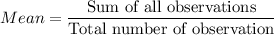
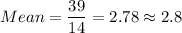
b) Median

`Median:\\\text{If n is odd, then}\\\\Median = \displaystyle(n+1)/(2)th ~term \\\\\text{If n is even, then}\\\\Median = \displaystyle((n)/(2)th~term + ((n)/(2)+1)th~term)/(2)`

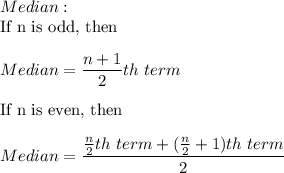
Sorted data:

1, 1, 1, 1, 2, 3, 3, 3, 4, 4, 4, 4, 4, 4

`\text{Median} = (7^(th)+8^(th))/(2) = (3+3)/(2) = 3`

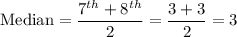
c) Mode

Mode is the observation with highest frequency. Since 4 appeared maximum time

Mode = 4

d) Mid range

It is the average of the smallest and largest observation of data.

`\text{Mid Range} = (1+4)/(2) = 2.5`

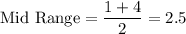
e) Measure of center

Option C) Only the mode makes sense since the data is nominal.