Answer:
2
Explanation:
To obtain the slope of the perpendicular line, we first have to identify the slope of the given line.
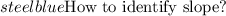
- In the slope- intercept form (y= mx +c), the coefficient of x is the slope of the line
- Do note that this is only true when the coefficient of y in the equation is 1
Given line: y= -½x +5
Slope of given line= -½
After finding the slope of the given line, we can now proceed to find the slope of the perpendicular line.
The product of the slope of two perpendicular lines is -1.
Let the slope of the perpendicular line be m.
m(-½)= -1
m= -1 ÷(-½)
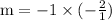
m= 2
Thus, the slope of the perpendicular line is
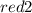 .
.
Other notes:
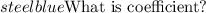
- Coefficient is the number that comes before a variable
- For example, in the case of 3x, the variable is x and the coefficient is 3