Question

What is the slope of a line that is perpendicular to the line y = -1/2x+ 5?

-2
O 3
O 2

Answer 1

2

Explanation:

To obtain the slope of the perpendicular line, we first have to identify the slope of the given line.

`\textcolor{steelblue}{\text{How to identify slope?}}`

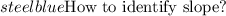
• In the slope- intercept form (y= mx +c), the coefficient of x is the slope of the line
• Do note that this is only true when the coefficient of y in the equation is 1

Given line: y= -½x +5

Slope of given line= -½

After finding the slope of the given line, we can now proceed to find the slope of the perpendicular line.

The product of the slope of two perpendicular lines is -1.

Let the slope of the perpendicular line be m.

m(-½)= -1

m= -1 ÷(-½)

`\text{m} = - 1 * ( - (2)/(1) )`

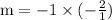
m= 2

Thus, the slope of the perpendicular line is
`\textcolor{red}{2}`.

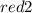Other notes:

`\textcolor{steelblue}{\text{What is coefficient?}}`

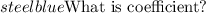
• Coefficient is the number that comes before a variable
• For example, in the case of 3x, the variable is x and the coefficient is 3