Question

Consider Compton Scattering with visible light.A photon with wavelength 500nm scatters backward(theta=180degree) from a free electron initially at rest.What is the fractional shift in wavelength delta\lamda/\lamda for the photon?

Answer 1

Answer:
`4.86(10)^(-12)m`

Step-by-step explanation:

The Compton Shift
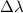`\Delta \lambda` in wavelength when photons are scattered is given by the following equation:

`\Delta \lambda=\lambda' - \lambda_(o)=\lambda_(c)(1-cos\theta)` (1)

Where:

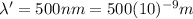`\lambda'=500 nm=500(10)^(-9) m` is the wavelength of the scattered photon

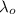`\lambda_(o)` is the wavelength of the incident photon

`\lambda_(c)=2.43(10)^(-12) m` is a constant whose value is given by
`(h)/(m_(e).c)`, being
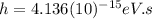`h=4.136(10)^(-15)eV.s` the Planck constant,
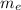`m_(e)` the mass of the electron and
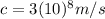`c=3(10)^(8)m/s` the speed of light in vacuum.

`\theta=180\°` the angle between incident phhoton and the scatered photon.

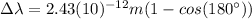`\Delta \lambda=2.43(10)^(-12) m (1-cos(180\°))` (2)

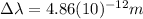`\Delta \lambda=4.86(10)^(-12)m` (3) This is the shift in wavelength