Question

Draw an angle in standard position whose terminal side contains the point

(7, −6).
Find the distance from the origin to this point.

Answer 1

The distance of the point from the origin = 9.29 units.

Explanation:

Given point:

(7,-6)

The angle lies such that the terminal side of the angle contains the given point.

To draw the angle and find the distance from the origin to the given point.

Solution:

The terminal side of the angle is where the angle ends with the initial side being the positive side of the x-axis.

So, we can plot the point (7,-6) by moving 7 units on the x-axis horizontally and -6 units on the y-axis vertically.

We can find the distance of the point from the origin by find the hypotenuse of the triangle formed.

Applying Pythagorean theorem.

`Hypotenuse^2=Shorter\ Leg^2+Shortest\ Leg^2`

`Hypotenuse^2 = (7)^2+(-6)^2`

`Hypotenuse^2=49+36\\Hypotenuse^2=85`

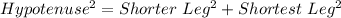
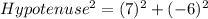
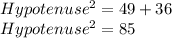
Taking square root both sides :

`√(Hypotenuse^2)=√(85)`

`Hypotenuse = 9.29\ units`

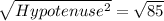
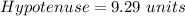
Thus, the distance of the point from the origin = 9.29 units.

The figure is shown below.