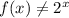Question

Describe and correct the error a student made in writing an exponential function

Starting value = 6
Constant ratio = 1/3

f(x) = 6(1/3)^x
f(x) = 2^x

Answer 1

The student made an error by applying the exponent to the product of a and b instead of just b. The final answer should be ​f(x)=6(1/3)^x

Explanation:

U can't multiply 6 by 1/3

Answer 2

we CANNOT DIVIDE 3 with 6.

Explanation:

Here,as given in the question:

Starting value = 6

Constant ratio = 1/3

Now, exponential function is obtained by the product of starting value and the constant ratio repeatedly.

⇒ f(x) = (Starting value) x (ratio)... x times

`\implies f(x) = 6 ((1)/(3) )^x = 6 ((1)/(3) ) ((1)/(3) ) ((1)/(3) ) .... x`

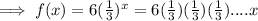
Now, we CANNOT DIVIDE 3 with 6 as it is in the power of x.

Hence,
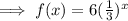`\implies f(x) = 6 ((1)/(3) )^x` and
`f(x) \\eq 2^x`