Answer:
Time taken by the sled is 1.31 s
Solution:
As per the question:
Coefficient of kinetic friction,
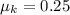
Velocity at point A,
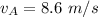
Velocity at point A,

Now,
To calculate the time taken by the sled to travel from A to B:
According to the impulse-momentum theorem, impulse and the change in the momentum of an object are equal:
Impulse, I = Change in momentum of the sled,
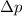 (1)
(1)
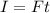 (2)
(2)
where,
F = Force
t = time
p = momentum of the sled
Force on the sled is given by:
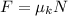
where
N = normal reaction force = mg
where
m = mass of the sled
g = acceleration due to gravity
Thus
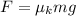 (3)
(3)
Using eqn (1), (2) and (3):
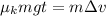
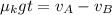

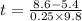
t = 1.31 s