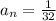Answer:
Recursive formula for geometric sequence
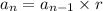
is
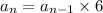
and explicit formula for geometric sequence
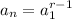 is
is
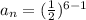
Explanation:
Given sequence is

To find the recursive and explicit formula for this sequence:
Let
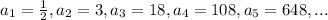
To find the common ratio r:
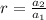
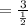
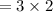

Therefore r=6
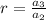
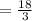

Therefore r=6
Therefore the common ration r=6
Therefore the given sequence is geometric sequence
Recursive formula for geometric sequence is
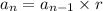
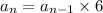
and explicit formula is
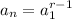
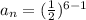
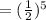
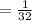
Therefore