Answer:
The answer is
![[(LX_1)/(46) + (L(1-x))/(18)]*0.454](https://img.qammunity.org/2021/formulas/chemistry/college/5tg6flcz3hqtdq72bwjrpdrp5dddn2ngbg.png) mol/hr
mol/hr
![[(Vy_1)/(46)+(V(1-y))/(18)]*0.454](https://img.qammunity.org/2021/formulas/chemistry/college/xl2p02uu0j9b742ucplhmqbudagm1uqgl2.png) mol/hr
mol/hr
Step-by-step explanation:
For flash distillation
F = V+L
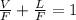
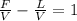
Fz = Vy+Lx
Y =
 let,
let,
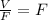
![y = (Z)/(F) -[ (1)/(F) -1]* X](https://img.qammunity.org/2021/formulas/chemistry/college/1y0cuq1z1qrqzfafm3ejqgsoumf6dao773.png)
Highlighted reading
F = 299;
 = 0.85 ; z = 0.36
= 0.85 ; z = 0.36
y =
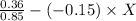
= 0.423 + 0.15x ------------(i)
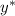 = -43.99713
= -43.99713
 + 148.27274
+ 148.27274
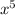 - 195.46
- 195.46
 +127.99
+127.99
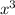 -43.3
-43.3
 + 7.469
+ 7.469
 + 0.02011
+ 0.02011
At equilibrium,
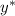 = y
= y
0.423+0.15
 =
=
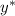
-43.99713
 + 148.27274
+ 148.27274
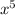 - 195.46
- 195.46
 +127.99
+127.99
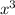 -43.3
-43.3
 + 7.319
+ 7.319
 -0.403
-0.403
F(x) for Newton's Law
Let
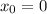
 =
=
![\frac{0-[{-0.403}]}{7.319}](https://img.qammunity.org/2021/formulas/chemistry/college/3phqunoy4b99jzk4rfwqb30ni63o7nw3l8.png)
= 0.055
 =
=
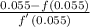
=
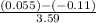
= 0.085
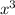 =
=
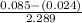
= 0.095
 =
=
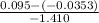
= 0.07
From This x and y are found from equation (i) and L and V are obtained from
 and F values
and F values
![[(LX_1)/(46) + (L(1-x))/(18)]*0.454](https://img.qammunity.org/2021/formulas/chemistry/college/5tg6flcz3hqtdq72bwjrpdrp5dddn2ngbg.png) mol/hr
mol/hr
![[(Vy_1)/(46)+(V(1-y))/(18)]*0.454](https://img.qammunity.org/2021/formulas/chemistry/college/xl2p02uu0j9b742ucplhmqbudagm1uqgl2.png) mol/hr
mol/hr