Question

Y=x^(2)-12x+40 in vertex form

Answer 1

`y=(x-6)^2+4`

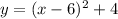
Explanation:

Vertex Form Of The Parabola

The equation of a parabola can be expressed in either standard or vertex form. The standard form is

`y=ax^2+bx+c`

and the vertex form is

`y=a(x-h)^2+k`

Where (h,k) it the vertex of the parabola

Transforming one into the other form is easily achieved by applying simple algebra .

Our function is

`y=x^2-12x+40`

Completing squares, we have

`y=x^2-12x+36+40-36`

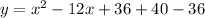
Reducing

`\boxed{y=(x-6)^2+4 }`

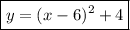
The vertex of the parabola is the point (6,4)