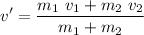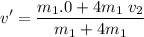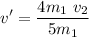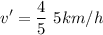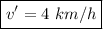Question

A railroad diesel engine weighs 4 times as much as a flatcar. If the engine coasts

at 5 km/h into a flatcar that is initially at rest, how fast do the two coast after
they couple together?

Answer 1

`\displaystyle v'=4\ km/h`

Step-by-step explanation:

Linear Momentum

The total linear momentum of an isolated system (with no external forces) is conserved regardless of the internal mutual interactions of its parts. Recall the momentum is obtained by multiplying the speed by the object's mass. We'll refer to the railroad diesel engine as mass 2 and the flatcar as mass 1.

We have the following data

`\displaystyle m_2=4\ m_1`

`\displaystyle v_1=0`

`\displaystyle v_2=5\ km/h`

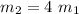
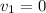
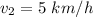
Since both objects remain coupled after their encounter, the final speed is common to both:

`\displaystyle v_1'=v_2'=v'`

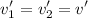
Let's sketch the principle of conservation of linear momentum as follows

`m_1v_1+m_2v_2=m_1v_1'+m_2v_2'`

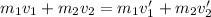
Using the mentioned conditions for the speeds

`\displaystyle m_1\ v_1+m_2\ v_2=(m_1+m_2)\ v'`

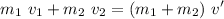
Solving for v'

`\displaystyle v'=(m_1\ v_1+m_2\ v_2)/(m_1+m_2)`

`\displaystyle v'=(m_1.0+4m_1\ v_2)/(m_1+4m_1)`

`\displaystyle v'=\frac{4\cancel{m_1} \ v_2}{5 \cancel{m_1}}`

`\displaystyle v'=(4)/(5)v_2`

`\displaystyle v'=(4)/(5)\ 5km/h`

`\boxed{\displaystyle v'=4\ km/h}`