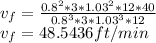Question

A 3-in-thick slab is 12 in wide and 15 ft long. Thickness of the slab is reduced in three steps in a hot rolling operation. In each step, thickness is reduced by 20% and width increases by 3%. If the entry speed of the slab in the first step is 40 ft/min, and roll speed is the same for the three steps, determine (a) length and (b) exit velocity of the slab after the final reduction.

Answer 1

`L_f=26.8108 ft`

Part B:

For Final Reduction

`v_f=48.5436ft/min`

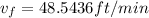
Step-by-step explanation:

Part A:

At each step 0.8 (100-20)% of thickness is left

Final Thickness t_f:

`t_f=(0.80)(0.80)(0.80)*3\\t_f=1.536 in`

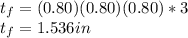
Width increases by 0.03 in each step so (100+3)%=1.03

Final Width w_f:

`w_f=(1.03)(1.03)(1.03)*12\\w_f=13.1127 in`

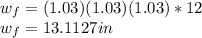
Conservation of volume:

`t_ow_oL_o=t_fw_fL_f\\L_f=(t_ow_oL_o)/(t_fw_f) \\L_f=(3*12*(15*12))/(1.536*13.1127)\\L_f=321.730 in\\L_f=26.8108 ft`

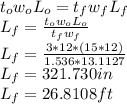
Part B:

`t_ow_ov_o=t_fw_fv_f`

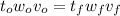
At First reduction exit Velocity:

`v_f=(t_ow_oL_o)/(t_fw_f) \\v_f=(3*12*(40))/(0.8*3*1.03*12)\\v_f=48.5439ft/min`

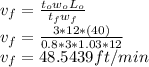
At 2nd Reduction:

`v_f=(0.8*3*1.03*12*40)/(0.8^2*3*1.03^2*12)\\v_f=48.5436ft/min`

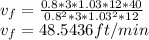
For Final Reduction:

`v_f=(0.8^2*3*1.03^2*12*40)/(0.8^3*3*1.03^3*12)\\v_f=48.5436ft/min`