Question

Ms. Lee wrote a test with 15 multiple choice short answer questions. The multiple choice questions x are worth 5 points and the short answer questions x are worth 10 points. The maximum number of points possible on the test is 100. Write a system of liner equations to represent this situation.

Answer 1

x + y = 15 and 5x + 10y = 100 are the system of equations that represent this situation

Solution:

Let "x" be the number of multiple choice questions

Let "y" be the number of short answer questions

Worth of 1 multiple choice questions = 5 points

Worth of 1 short answer question = 10 points

Ms. Lee wrote a test with 15 multiple choice short answer questions

Therefore,

number of multiple choice questions + number of short answer questions = 15

x + y = 15 -------- eqn 1

The maximum number of points possible on the test is 100

Therefore, we frame a equation as:

number of multiple choice questions x Worth of 1 multiple choice questions + number of short answer questions x Worth of 1 short answer question = 100

`x * 5 + y * 10=100`

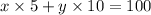
5x + 10y = 100 ------- eqn 2

Thus eqn 1 and eqn 2 are the system of equations that represent this situation