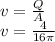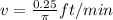Answer:
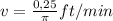
Explanation:
There is a relation with the initial and final dimensions of the hopper according to the sand level when its high is 6 feet as follows:
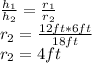
Where the calculated
 is given with the 6 feet hgh.
is given with the 6 feet hgh.
Then we have the sand flow formula which is:
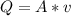
Where A represents the area of the transversal section and v the velocity that we need to know, the area is:
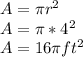
And finally the sand is dropping when the level is 6 feet high with the velocity (v) :