Question

At time t = 0, a football player kicks a ball from the point A with position vector (2i + j) m on a horizontal football field. The motion of the ball is modelled as that of a particle moving horizontally with constant velocity (5i + 8j) m s–1.

Find


(a) the speed of the ball,

(b) the position vector of the ball after t seconds.


The point B on the field has position vector (10i + 7j) m.

(c) Find the time when the ball is due north of B.


At time t = 0, another player starts running due north from B and moves with constant speed v m s–1. Given that he intercepts the ball,


(d) find the value of v.


(e) State one physical factor, other than air resistance, which would be needed in a refinement of the model of the ball’s motion to make the model more realistic.

Answer 1

To solve these physics problems, we used vector mathematics to find the speed of the ball, its position after a certain time, the time it aligns with a certain point, and the speed of a player to intercept it. Additionally, we considered gravity as a factor for a more realistic model of the ball's motion.

Step-by-step explanation:

Speed of the ball: To find the speed of the ball, we calculate the magnitude of the velocity vector (5i + 8j) m/s using the Pythagorean theorem, which results in \(\sqrt{5^2 + 8^2} = \sqrt{89}\) m/s.

Position vector after t seconds: We calculate the position vector at time t by using the initial position vector (2i + j) m and adding the product of the velocity vector and time t. This yields the formula (2i + j) + t(5i + 8j).

Time when the ball is due north of B: For the ball to be due north of B, their i-components must be equal. Given B's position vector is (10i + 7j), we set the i-component equal to 10 and solve for t, getting t = (10 - 2)/5 = 1.6 seconds.

Value of v for the running player: Since the player intercepts the ball after 1.6 seconds, and the ball's j-component of the velocity is 8 m/s, the player's velocity v must be the distance covered in the j direction divided by time, which is (8j - 7j)/1.6 = 0.625 m/s.

Physical factor for a more realistic model: One physical factor to make the model more realistic could be the effect of gravity on the ball's trajectory, which would cause the ball to follow a parabolic path rather than a straight line.

Answer 2

a) 9.434 m/s

b) i (2+5*t) + (1+8*t-4.905*t²) j

c) t= 8/5 secs

d) 3.598 m/s

e) See explanation

Step-by-step explanation:

Part a)

The speed of the ball can be calculated from the given velocity v = 5i +8j

Taking magnitude of v = 5i + 8j

magnitude (v) =
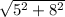`√(5^2 + 8^2)` = 9.434 m/s.

Part b)

Using kinematic equation of particle as follows:

Sf = Si + Vi*t + 0.5*a*t² ..... Eq 1

Given: Si = (2i + j) m ; Vi = (5i+8j) m/s; a = -9.81 j m/s²

We evaluate Eq 1:

Sf = (2i+j) + (5i+8j)*t + 0.5*(-9.81j)*t²

We get after combining similar terms:

Sf = i (2+5*t) + (1+8*t-4.905*t²) j ..... Eq 2

Part c)

Using kinematic equation of particle only in i axis as follows we use Eq 1:

Sf = Si + Vi*t + 0.5*a*t²

Given: Si = 2 m ; Sf = 10; Vi = 5 m/s; a = 0;

We evaluate Eq 1:

10 = 2 + 5*t - Solve for t

t = 8/5 seconds

Note: The above is the time t when the ball is due north of (10i+7j) i.e having a position vector of 10 in east direction but unknown in north direction. A point directly above or below 10i + 7j.

Part d)

The interception of ball and the player occurs at the same t = 8/5 secs and @ position vector (10i + aj) where a is a constant needs to be found.

Find a:

Using Eq 2 found in part b:

Sf = i (2+5*t) + (1+8*t-4.905*t²) j

Evaluate @ t= 8/5 secs

Sf = (10) i + (1.2432) j .... Eq 3

To find the speed v of the player when he intercepts the ball at Sf = (10) i + (1.2432) j is evaluated as follows:

v = change in position of player / Time

`v =(Eq 3 - (10i+7j))/(1.6)`

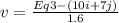
Hence, v = -3.598 j = 3.598 m/s

Part e)

Friction between the ball and surface from which is launched.