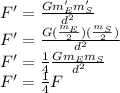Answer:
Reduce the mass of the earth to one-fourth its normal value.
Reduce the mass of the sun to one-fourth its normal value.
Reduce the mass of the earth to one-half its normal value and the mass of the sun to one-half its normal value.
Step-by-step explanation:
Every particle in the universe attracts any other particle with a force that is directly proportional to the product of its masses and inversely proportional to the square of the distance between them. So, in this case we have:
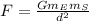
If
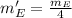 :
:

If
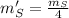

If
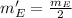 and
and
 :
: