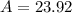Answer:
23.92
Explanation:
We solve for y:
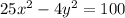
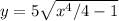
use trig substitution:
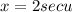
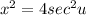
The derivative of x is:
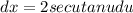
when x=2
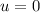
when x=3
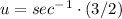
The area is defined as 2xarea:
The area is the integral of the equation:
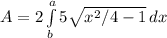 for range 0 to sec-1(3/2)
for range 0 to sec-1(3/2)
Substitute x=2secu
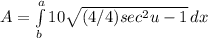
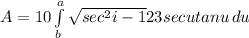
We know that sec²-1 = tan²u
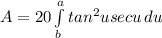
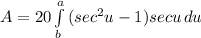
![A=20[\int\limits^a_b {sec^3u} \, du - \int\limits^a_b {secu} \, du]](https://img.qammunity.org/2021/formulas/mathematics/college/1q38b11jatbwm902xj8nnjo4t6i2gnchem.png)
After simplifying
![A=10[secutanu-ln(secu+tanu)]](https://img.qammunity.org/2021/formulas/mathematics/college/nmvjlup8udguoxlcptiuw93ze51ectf1ir.png)
For the range
![A=10[(3/2)√(5) /2-ln(3/2+√(5)/2)]](https://img.qammunity.org/2021/formulas/mathematics/college/sk7su0ccoekfklrumvxgmfl42d6vahtl0g.png)