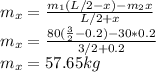Question

Ricardo, of mass 80 kg, and Carmelita, who is lighter, are enjoying Lake Merced at dusk in a 30 kg canoe. When the canoe is at rest in the placid water, they exchange seats, which are 3.0 m apart and symmetrically located with respect to the canoe's center. If the canoe moves 40 cm horizontally relative to a pier post, what is Carmelita's mass?

Answer 1

m=57.65 kg

Step-by-step explanation:

Given Data

Ricardo mass m₁=80 kg

Canoe mass m₂=30 kg

Canoe Length L= 3 m

Canoe moves x=40 cm

When Canoe was at rest the net total torque is zero.

Let the center of mass is at x distance from the canoe center and it will be towards the Ricardo cause. So the toque around the center of mass is given as

`m_(1)(L/2-x)=m_(2)x+m_(2)(L/2-x)`

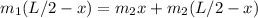
We have to find m₂.To find the value of m₂ first we need figure out the value of.As they changed their positions the center of mass moved to other side by distance 2x.

so

2x=40

x=40/2

x=20 cm

Substitute in the above equation we get

`m_(x)=(m_(1)(L/2-x)-m_(2)x )/(L/2+x)\\m_(x)=(80((3)/(2)-0.2 )-30*0.2)/(3/2+0.2)\\m_(x)=57.65 kg`