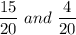Question

Explain how to find a common denominator of 3/4 and 1/5 what is a common denominator of 3/4 and 1/5 show how you can rename 3/4 and 1/5 using that common denominator

Answer 1

Common denominator = 20

New fractions are:
`(15)/(20)\ and\ (4)/(20)`

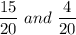
Explanation:

Given:

The fractions are given as:

`(3)/(4)\ and\ (1)/(5)`

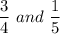
The denominators of the first fraction is 4 and that of the second fraction is 5.

In order to find the common denominator for 4 and 5, we have to find the least common multiple of each of the numbers.

Multiples of 4 = 4, 8, 12, 16, 20, 24, 28,....

Multiples of 5 = 5, 10, 15, 20, 25, 30,....

Therefore, the least common multiple of 4 and 5 is 20. So, the common denominator is 20.

Now, multiply the numerator and denominator of each fraction by the same suitable number such that the denominator becomes 20.

So, for the first fraction, 4 is in the denominator.

So, 4 when multiplied by 5 gives 20.

So, we multiply the numerator and denominator of first fraction by 5. This gives,

`(3)/(4)=(3* 5)/(4* 5)=(15)/(20)`

Now, for the second fraction, 5 is in the denominator.

So, 5 when multiplied by 4 gives 20.

So, we multiply the numerator and denominator of first fraction by 4. This gives,

`(1)/(5)=(1* 4)/(5* 4)=(4)/(20)`

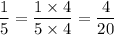
Therefore, the new fractions after making the denominators same are:

`(15)/(20)\ and\ (4)/(20)`